Using Cuckoo Hashing to Implement Pair Kerning

Whenever I hear the word cuckoo, Miloš Forman's great movie comes to my mind. But lately, I have built a new association for this word. I have been hacking on JagPDF and needed a compact data structure with fast lookup to represent font kerning metrics. After some research I ended up with an open-address hashing method called cuckoo hashing.

Well, it turned out that it was a good choice. This post describes the details on how I used this method to build a static hash table having very good characteristics. I achieved the load factor above 0.9 with lookups executing on average less than 70 machine instructions.

The idea is applicable generally, not only for kerning metrics, and it is an interesting alternative to perfect hashing.

Kerning

For those unfamiliar with kerning, it is the process of adjusting letter spacing in a proportional font. Generally, a font may provide a table which maps glyph pairs to an offset. When a text formatting application positions text, it looks adjacent glyphs up in the table and if found then the associated offset is added to the default character spacing. For instance, there are two kerning pairs in the following text: Ke and rn.

Click the text to toggle kerning (requires JavaScript).

Let's clarify the relationship among the following terms which will be used in the rest of this post:

kerning pair = code point pair + kerning offset

kerning metrics = a set of kerning pairs

Goal

JagPDF supports so called PDF core fonts. The PDF reference guarantees that these fonts are always present which implies that their metrics have to be embedded into the JagPDF. So, the goal is to implement:

• a compact memory representation of the kerning metrics,
• a lookup function that for a given core font and a code point pair retrieves a kerning offset.

Memory Representation of Kerning Metrics

There are 14 core fonts but only 8 of them provide kerning information. Intuitively, there should be a lot of repeating data, so let's analyze the kerning metrics¹:

number of all kerning pairs	19046
number of unique code point pairs	3260
code points	⊂ {32, ..., 8221}
number of unique offset values	59
offset values	⊂ {-180, ..., 92}
number of kerning pairs per font	2705, 2321, 2481, 2038, 2481, 2705, 2073, 2242

The table confirms that many same code point pairs repeat in the fonts. That suggests that a joint lookup table could be used for all fonts. Even though it increases the search space for each lookup by 27% on average, it is a fair trade-off as it saves 83% of memory that would be otherwise needed for the code point pairs².

As all code points fall into {32, ..., 8221}, a code point pair can be encoded to a 32-bit integer key, using lower 16 bits for the left code point and higher 16 bits for the right one.

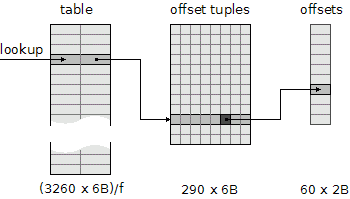
A key is associated with an offset tuple, which is an array of 8 offset values, one for each font. It turned out that there are only 290 unique tuples. This allows us to reference tuples indirectly, using 2 bytes per a tuple, and thereby to save at least 58% of memory needed for the tuples otherwise.

Finally, as to actual kerning offsets, there are only 60 distinct ones³. Using an indirection, an offset can be represented by a 6-bit index, which makes the offset tuple 6 bytes long.

As the picture shows, to represent the complete kerning information for the core fonts, at least 19560 / f + 1860 bytes is needed, where f is from (0, 1> and is called the load factor. The load factor expresses the ratio of the number of the keys to the table capacity.

Lookup Function

Let's focus on the lookup function now. A string of length N requires N-1 lookups. The following table shows the frequency of occurrence of kerning pairs in several texts.

text	length (N)	#pairs/(N-1)
The Hound of the Baskervilles	316874	0.13
Oliver Twist	893948	0.15
The Critique of Pure Reason	1258719	0.12
< /dev/urandom tr -dc 'A-Za-z0-9,.()' | head -c1048576	1048575	0.05

The important points about the lookup function are:

• It could easily become a performance bottleneck because of the expected high number of invocations.
• On average, only every 7-th lookup is successful. So ideally, it should be optimized for unsuccessful cases.

Cuckoo Hashing

If you have never heard of cuckoo hashing, this introductory article can help you to understand the basic concept. Quoting from that article:

The basic idea is to use two hash functions instead of only one. This provides two possible locations in the hash table for each key.

When a new key is inserted, a greedy algorithm is used: The new key is inserted in one of its two possible locations, "kicking out", that is, displacing any key that might already reside in this location. This displaced key is then inserted in its alternative location, again kicking out any key that might reside there, until a vacant position is found, or the procedure enters an infinite loop. In the latter case, the hash table is rebuilt in-place using new hash functions.

According to the authors⁴, keeping the load factor slightly under 0.5 ensures that insertions should succeed in O(1). We can aim for a higher factor because the table is static and thereby having unconstrained time on insertions.

There are variations on the basic idea which improve the load factor. One is to use more hash functions which increases the number of possible locations for a key. Another one is to split buckets into multiple cells, and thereby store multiple keys per bucket.

Since the lookup function is required to be fast, I chose hashing by division. It turned out that it is good enough since using a different class of hash functions (e.g. universal) did not yield a better load factor. So, the class H of the used hash functions is:

h_p(k) = k mod p

H = {h_p : p is a prime number}

To be able to test cuckoo hashing behavior with various parameters, I wrote the following Python cuckoo table builder:

class CuckooNest:
    def __init__(self, nr_buckets, hash_funs, nr_cells=1):
        self.nr_buckets = nr_buckets
        self.hash_funs = hash_funs
        self.nr_cells = nr_cells
        self.table =  nr_cells * nr_buckets * [None]
        self.nr_items = 0

    def cells(self, n, key):
        """Calculate hash using n-th hash function and return a list of cell
        indices."""
        pos = self.hash_funs(n, key) % self.nr_buckets
        return [self.nr_cells * pos + n for n in range(self.nr_cells)]

    def insert(self, key, value):
        cells = self.cells(0, key)
        item = (key, value)
        for n in xrange(self.nr_items + 1):
            for cell in cells:
                if None == self.table[cell]:
                    self.table[cell] = item
                    self.nr_items += 1
                    return
            p0 = random.choice(cells)
            item, self.table[p0] = self.table[p0], item
            all_cells = [self.cells(i, item[0]) for i in range(len(self.hash_funs))]
            all_cells.remove(cells)
            cells = random.choice(all_cells)
        raise TableFull('cannot insert %d' % item[0])

    def load_factor(self):
        return float(self.nr_items) / len(self.table)

Notes on CuckooNest:

• It can hash using two and more hash functions.
• It allows multiple cells per bucket. For instance in case of two cells per bucket, a key hashed to k-th bucket can be inserted either to location 2k or to 2k+1.
• The insert operation raises a TableFull exception if it cannot insert an item. In the same situation, the standard version could resize the table, and it would rehash the items with different hash functions.
• The insert operation is randomized for three and more hash functions, or two or more cells per bucket.

Now that we have CuckooNest, we can start with experiments. The following function performs binary search on nr_buckets_lst to find the minimal number of buckets needed to insert input_data (i.e. without raising TableFull).

def maximize_load_factor(N, input_data, nr_buckets_lst, hfun_gen, nr_cells):
    low, high = 0, len(nr_buckets_lst)
    reset = True
    while high > low:
        if reset:
            max_factor, curr_max_factor = 0.0, 0.0
            nr_tries = N
            mid = low + (high - low) / 2
        else:
            max_factor = curr_max_factor
            nr_tries *= 2
        found = False
        for i in xrange(nr_tries):
            hfuns = hfun_gen.next()
            htable = CuckooNest(nr_buckets_lst[mid], hfuns, nr_cells)
            try:
                for key, val in input_data:
                    htable.insert(key, val)
                print 'OK:', nr_buckets_lst[mid], htable.load_factor(), hfuns
                high = mid - 1
                found = True
                break
            except TableFull:
                curr_max_factor = max(curr_max_factor, htable.load_factor())
        if not found and curr_max_factor > max_factor:
            reset = False
        else:
            reset = True
            if not found:
                low = mid + 1

In each step, the algorithm performs a brute force search for hash functions that do not cause raising TableFull for the given number of buckets and input_data.

A search step proceeds in iterations, trying 2^k-1N random hash functions in k-th iteration. The step either ends with success, or fails if the last achieved load factor is lower than the one in the previous iteration.

Results

I fed maximize_load_factor with the kerning metrics and tried various combinations of the hashing parameters. Then I generated the best hash tables for each parameter combination to C++ and tested the performance of the lookup function on The Hound of the Baskervilles. I used callgrind to collect the number of executed instructions (Ir). Here are the results:

hash functions	cells per bucket	load factor	average Ir
2	1	0.62	62.0
3	1	0.93	91.0
2	2	0.92	68.9

Obviously, what we see is the classic space vs. speed trade-off. The increasing number of hash functions and cells improves the load factor but slows the lookup function down.

Anyway, for me the (2, 2) variant was a fairly clear choice. Here is the summary of the solution I used in JagPDF:

• The hash table has 3,554 cells (i.e 1,777 buckets) and stores 3,260 keys, which means the load factor 0.92.
• On the whole, 23,202 bytes is needed to store 19,046 kerning pairs, which is 1.22 bytes per kerning pair.
• The lookup function executes on average 69 instructions per lookup on the x86 architecture.

For the sake of completeness, here is the winning lookup function:

int t1_get_kerning(t1s_face const& face, Int left, Int right)
{
    if (!face.get_kerning)
        return 0;

    boost::uint32_t key = (left & 0xffff) + (right << 16);
    const kern_rec_t *loc =
        kerning_table + 2 * ((key % 1984061) % 1777);

    if (loc->key != key && (++loc)->key != key)
    {
        loc = kerning_table + 2 * ((key % 885931) % 1777);
        if (loc->key != key && (++loc)->key != key)
            return 0;
    }

    int val = (*face.get_kerning)(kerning_offsets[loc->offset_index]);
    return kern_values[val];
}

If you are interested in details, t1_get_kerning() is defined in t1adobestandardfonts.cpp (along with the generated metrics). The Python code related to cuckoo hashing is buried in afm_parser.py.

Other Methods

Perfect hashing

There are two mature perfect hashing function generators I know of: gperf and cmph. However, it seems that the result achieved with cuckoo hashing is better than I would probably get with these generators. It does not mean that my approach is superior to these methods, I just had unconstrained time to find the hash functions, whereas e.g. cmph generates perfect hash functions in O(N). An additional complication is that, as far as I know, both gperf and cmph operate only on string keys.

mkhashtable

mkhashtable is a tool for generating integer lookup tables using cuckoo hashing. It implements the standard cuckoo hashing with two symmetric tables. Running it on the kerning metrics with -E and -i 15000 gives the load factor 0.62 which corresponds to my results.

Binary search

Binary search would enable the most possible compact memory representation, i.e. the load factor 1.0. For the 3,260 kerning pairs, the lookup would cost at most 12 comparisons. Unfortunately, that worst case would be quite frequent. Testing revealed that the binary search is on average 2.2 times slower than the selected solution. A combination with the Bloom filter may possibly speed it up since the Bloom filter could filter out some of the unsuccessful lookups, but I did not test this.

Try it out

If your favorite programming language is among those supported by JagPDF, you can try this new feature out. To turn kerning on just set the text.kerning option to 1. Here is an example in Python:

import jagpdf

profile = jagpdf.create_profile()
profile.set("text.kerning", "1")
doc = jagpdf.create_file('kerning.pdf', profile)
doc.page_start(200, 200)
doc.page().canvas().text(80, 100, "Kerning")
doc.page_end()
doc.finalize()

Quiz

Let's conclude this post with an eyeball exercise. The following two PDF files, generated by JagPDF, show one page of the very same text. One file was generated with kerning enabled while the second one with kerning turned off. Do you tell which one is which?

text-1.pdf

text-2.pdf

Footnotes

[1]	The metrics for the core fonts are available from Adobe's Developer Resources.

[2]	This should incur no performance penalty for an O(1) lookup and even for an O(log2N) lookup it is at most one extra comparison for some fonts.

[3]	Even though there is 59 distinct offset values, the size of the offset array is 60, since the zero offset is needed for fonts that do not define kerning for a given pair.

[4]	http://citeseerx.ist.psu.edu/viewdoc/summary?doi=10.1.1.25.4189